Esoma-KE Logo
esoma@esomake.co.ke
Change Class  |  Change Subject

Measurement - Length, Area, Volume, Density and SI Units

  Change Class FORM ONE
Select Subject  |  Physics

PHYSICS REVISION QUESTIONS

Click to Attempt Form 1 Physics Questions




Want to enjoy learning? Try reading without Ads!

Say goodbye to distractions and enjoy uninterrupted learning with our new ad-free feature. Dive into our vast collection of educational content without any interruptions.

Explore Ad-Free learning plus lots of other premium benefits for as little as KES 200 per month.
Click to Join Now→




Measurement comprises of length, area, volume, mass, density and time.

SI Units

Universal System of Units is called system international d' unites (International System of Units) - SI Units.
Below are the major SI Units
Basic Quantity SI Unit Symbol
Length Metre m
Mass Kilogram kg
Time Second s
Electric Current Ampere A
Thermodynamic Kelvin K
Luminous Intensity Candela Cd
Amount of Substance Mole mol

LENGTH

- The distance between two fixed points.
- The S.I Unit is Metre (M)
Derived units are shown below
Unit Symbol Equivalence in Metres
Kilometre Km 1000
Hectometre Hm 100
Decametre Dm 10
Decimetre dm 0.1
Centimetre Cm 0.01
Millimetre mm 0.001
Micrometre µm 0.000001

Estimating the length of a tree

Ready? Attempt these Physics > Measurement 1 Questions (Answers Available)

AREA

- Measures the surface area covered by a body
- Its unit is m2.
Can you convert 15.5M2 to cm2?

Solution
1m = 100 cm
1m2 = 100 cm x 100 cm = 10000 cm2
15.5 m2 = 15.5 x 10000 cm2
= 1550000 cm2



Area of a Regular Body

Regular Body Formulae
Square L x L
Rectangle L x W
Circle πr2
Triangle ½bh
Cylinder 2πDh
Trapezium ½(a+b)h

Remember that π = 22/7 or 3.1429

Area of an Irregular Body

The squares must be 1cm2 each.

Area
Full Squares = .... cm2
½ x Incomplete squares = .... cm2
Area = Full Squares + (½ x Incomplete squares)

VOLUME

- Measures the amount of space occupied by a body
- Its unit is m3.
Can you convert 4.5m3 to cm3 ?

Remember: 1m3 = 100cm x 100cm x 100cm = 1000000 cm3


Volume of a Regular Body

Regular Body Formulae

Cube


 V = S3

Rectangular Prism


 V = l x w x h

V = Bh

Sphere


 V = 4/3πr3

Right Circular Cylinder


 V = πr2h

Right Circular Cone


 V = 1/3πr2h

Right Square Pyramid


 V = 1/3S2h
NB: Liquids can be measured by putting them into containers with sizes of graduated objects such as Graduate Cylinder, Syringe, Buret and others


Volume of an Irregular Body

It can be done using a Measuring Cylinder or a Eureka Can.
1. Measuring Cylinder

Volume = Q (V1) - P (V2)


2. Eureka Can

Volume will be read on the measuring cylinder.

MASS

- Quantity of matter in a body. SI units is Kilogrammes (Kg)
Mass can be measured using:-
  • Top Pan Balance
  • Beam Balance
  • Lever Balance

DENSITY

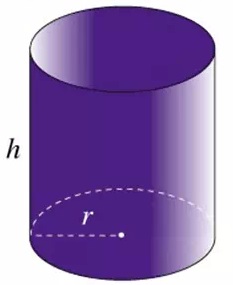
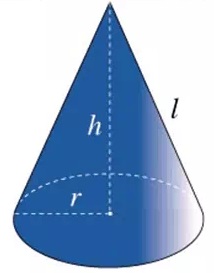
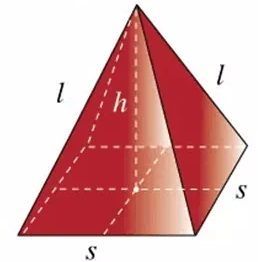
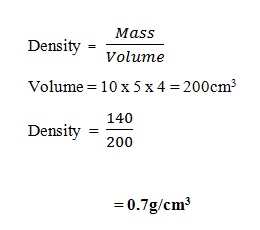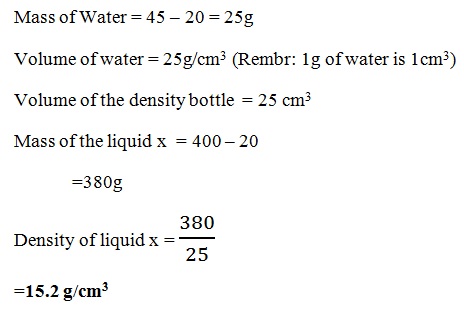- Mass per unit volume. Its symbol is rho (ρ). Its SI Unit is Kilogramme per Cubic Metre (Kg/m3)
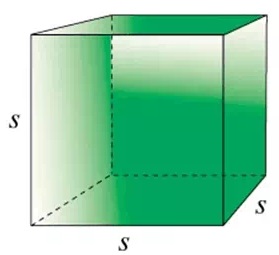
A block of stone has a mass of 140g and is 10cm long, 5 cm wide and 4 cm high. Calculate the density of the stone

Solution


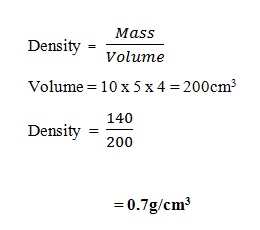
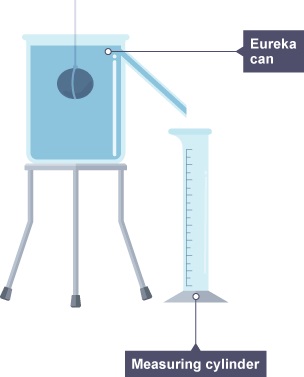
Density Using a Density Bottle
The mass of a density bottle is 20g when empty and 45g when filled with water. When filled with liquid x, its mass is 400g. Calculate the density of liquid x. (density of water 1.0 g/cm3)

Solution



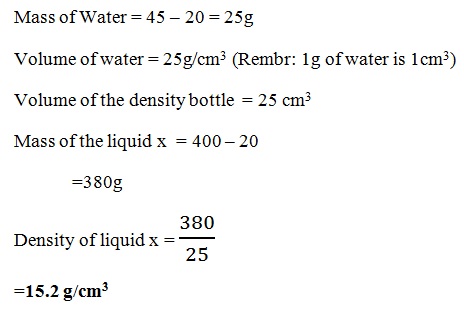
Relative Density

Relative density (RD) is the ratio of the density of a substance to the density of water. It is also known as specific gravity (SG).
- If the value is less than 1, it is less dense than water and would float
- If the value is equals to 1, it has the same density as water
- If the value is greater than 1 it is more dense than water and would sink.


 

Measurement I Quiz 1

Question - of -

 
 
 
Previous Next

Hello Esoma-KE Member, please help review these notes.    Why review


Very Poor Poor Good

Very Good Excellent
Your review has been successfully submitted.
Tell us what you think about the notes.

Submit Comment

Students' and Teachers' Reviews


Here's what our users had to say ...

Guest User
Good notes keep it up
Guest User
good