Uniform Circular Motion - High School Physics Form 4

This motion can be described as the motion of a body moving along a circular path by giving the angle covered in a certain time along the path of motion. The angle covered in a certain time is proportional to the distance covered along the path of motion.

One radian is the angle subtended at the centre of the circle by an arc of length equal to the radius of the circle. Since one circle = 3600
and has 2 π radianstherefore 1 radian = 3600/ 2 π r=
57.2960
or 57.30

Example

A wheel of radius 50 cm is rolled through a quarter turn. Calculate
(i) The angle rotated in radians
(ii) The distance moved by a point on the circumference.
Solution
(i) A quarter turn = 3600/ 4= 900
. Since 3600
= 2 π radians.
Alternately since 1 radian = 57.30
hence 900
= 1.57 radii.
(ii) A point on the circumference moves through an arc,
Arc = radius ×θ (θ in radians)
= 50 cm × 1.57
= 78.5 cm.

If a body moving in a circular path turns through an angle θ radians in time ‘t’, we define angular velocity omega (ω), as the rate of change of the angle θ with time.
ω= θ / t, unit for angular velocity is radians per second (rads-1). Since the radian measure is a ratio we can write it as second-1(s-1). We can establish the relationship between angular velocity ‘ω’ and linear velocity ‘v’, from the relation, θ = arc / radius, arc = radius × θ.
Dividing the expression by ‘t’, then arc / t = radius, but arc / t = v (angular velocity). So ‘v’ = radius × ω. This expression gives us the relationship between angular and linear velocity.

<

If the angular velocity for a body changes from ‘ω1’ to ‘ω2’, in time ‘t’ then the angular acceleration, α can be expressed as; α= (ω2 – ω1) / t
Units for angular acceleration are radians per second squared (rad s-2) or second-2(s-2). When α is constant with time, we say the body is moving with uniform angular acceleration.
Note: In uniform circular motion α is equal to zero.
To establish the relationship between angular acceleration and linear acceleration, from the relation, v = radius × ω, then dividing by ‘t’, we get (v / t) = radius × ω / t..
But v / t = a (linear acceleration) and ω / t = α (angular acceleration).
So a = radius × α.

This is a force which acts on a body by directing the body towards its centre. Since the direction is continuously changing, the velocity therefore cannot be constant.
Applying Newton’s law of motion (F = ma), the centripetal force Fc is given by;
Fc = ma = mv²
/R. Since v = radius ω, then
Fc = mv² – ω²
/R = mRω².
The centripetal acceleration ‘a’ in relation to angular velocity, ω, is given by a = Rω2

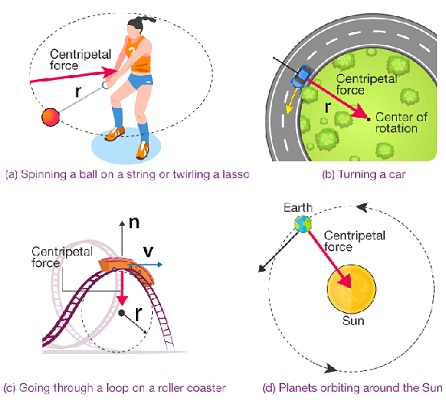
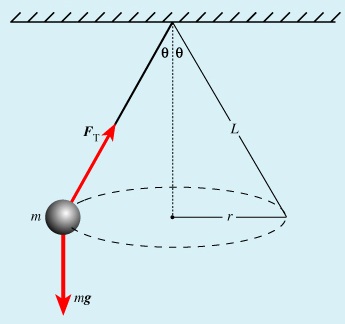
Consider a mass ‘m’ tied to a string of length ‘r’ and moving in a vertical circle as shown below.
At position 1– both weight (mg) and tension T are in the same direction and the centripetal force is provided by both, hence T1 + mg = mv²/r. T1 = mv²/r – mg.(The velocity decreases as T1decreases since mg is constant).T1will be zero when mv²/r = mg and thus v = √ – this is the value of minimum speed at position 1 which keeps the body in a circle and at this time when T = 0 the string begins to slacken.
At position 2– the ‘mg’ has no component towards the centre thus playing no part in providing the centripetal force but is provided by the string alone.
T2 = mv²/r

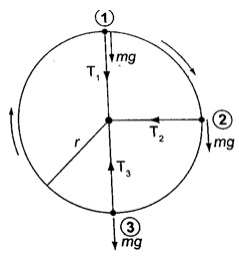
At position 3– ‘mg’ and T are in opposite directions, therefore;
T3 – mg = mv2/r; T3 = mv2/r + mg– indicates that the greatest value of tension is at T3 or at the bottom of the circular path

Examples

1. A ball of mass 2.5 × 10-2 kg is tied to a string and whirled in a horizontal circular path at a speed of 5.0 ms-2
If the string is 2.0 m long, what centripetal force does the string exert on the ball?
Solution
Fc = mv2/r = (2.5 × 10-2) × 52/ 2.0 = 0.31 N.

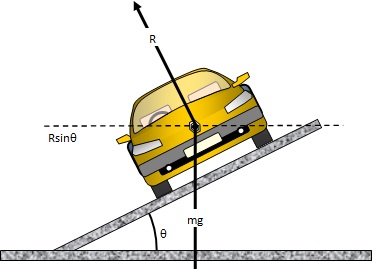
2. A car of mass 6.0 × 103kg is driven around a horizontal curve of radius 250 m. if the force of friction between the tyres and the road is 21,000 N. What is the maximum speed that the car can be driven at on a bend without going off the road?
Solution
Fc = force of friction = 21,000, also Fc = mv2/r, hence
21,000 = (6.0 × 103) × v2/ 250, v2= (21,000 × 250) /6.0 × 103

3. A stone attached to one end of a string is whirled in space in in a vertical plane. If the length of the string is 80 cm, determine the minimum speed at which the stone will describe a vertical circle. (Take g = 10 m/s2).
Solution
Minimum speed v = √ = √ × 10 = 2.283 m/s.

It consists of a small massive object tied to the end of a thin string tied to affixed rigid support. The object is then pulled at an angle then made to whirl in a horizontal circle.
When speed of the object is constant the angle θ becomes constant also. If the speed is increased the angle θ increases, that is the object rises and describes a circle of bigger radius. Therefore as the angular velocity increases ‘r’ also increases.

It consists of a small metal container tubes which can be electrically or manually rotated in a circle. If we consider two particles of different masses m1and m2 each of them requires a centripetal force to keep it in circular motion, the more massive particle require a greater force and so a greater radius and therefore it moves to the bottom of the tube.
This method is used to separate solids and liquids faster than using a filter paper

As a vehicle moves round a bend, the centripetal force is provided by the sideways friction between the tyres and the surface, that is; Centripetal force = mv²/r = frictional force To enable a vehicle to turn along a bend at high speed the road is raised on the outer edge to attain a saucer-like shape and this is known as banking, where part of the centripetal force necessary to keep the vehicle on track is provided by the weight of the vehicle. This allows cars to negotiate bends at critical speeds.

1. Centrifuges

they are used to separate liquids of different densities i.e. cream and milk

2. Drying clothes in spin dryer

clothes are placed in a perforated drum rotated at high speed, water is expelled through the holes and this makes the clothes dry.

3. Road banking

especially for racing cars which enables them to move at critical speed along bends without going off the tracks.

4. Speed governor

the principle of conical pendulum is used here to regulate the speed by controlling the fuel intake in the combustion chamber. As the collar moves up and down through a system of levers it thereby connects to a device which controls the fuel intake.