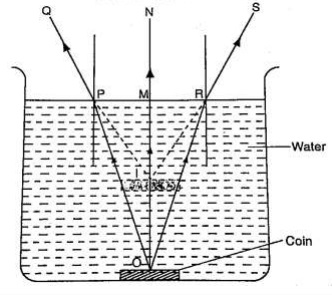
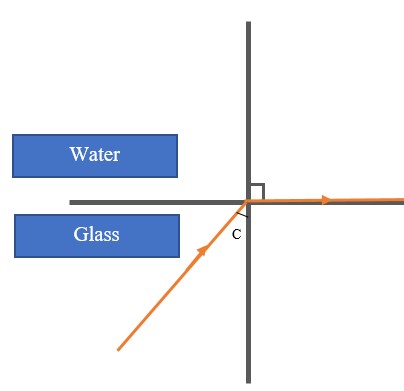
Explanation: To investigate the path of light through rectangular glass block.
Apparatus: - soft-board, white sheet of paper, drawing pins (optical), rectangular glass block.
Procedure
- Fix the white plain paper on the soft board using pins
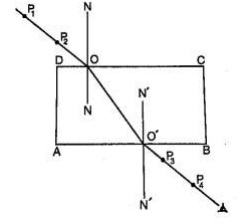
- Place the glass block on the paper and trace its outline, label it ABCD as shown below
- Draw a normal NON at point O
- Replace the glass block to its original position
- Stick two pins P1 and P2 on the line such that they are at least 6cm apart and upright
- Viewing pins P1 and P2 from opposite side, fix pins P3 and P4 such that they’re in a straight line
- Remove the pins and the glass block
- Draw a line joining P3 and P4 and produce it to meet the outline face AB at point O
- Light travels at a velocity of 3.0 & 108 in a vacuum.
- Light travels with different velocities in different media.
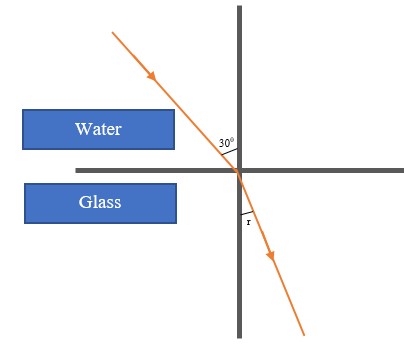
- When a ray of light travels from an optically less dense media to more dense media, it is refracted towards the normal.
- The glass block experiment gives rise to a very important law known as the law of reversibility which states that "if a ray of light is reversed, it always travels along its original path".
- If the glass block is parallel-sided, the emergent ray will be parallel to the incident ray but displaced laterally as shown
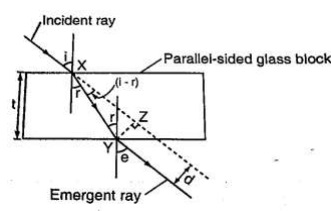
The direction of the light is not altered but displaced sideways.
This displacement is called lateral displacement and is denoted by 'd'. Therefore
XY = t/Cos r, YZ = Sin (i - r) × x y
So, lateral displacement, d = t Sin (i - r)/Cos r
Laws of Refraction
- The incident ray, the refracted ray and the normal at the point of incidence all lie on the same plane.
- The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a
constant for a given pair of media.
Sin i/sin r = constant (k)
Refractive index
Refractive index (n) is the constant of proportionality in Snell's law: henceSin i/ sin r = n
Therefore sin i/sin r = n = 1/sin r/sin i
Example 1
Calculate the refractive index for light travelling from glass to air given that ang = 1.5
Solution
gna= 1/ang = 1/1.5 = 0.67
Calculate the angle of refraction for a ray of light from air striking an air-glass interface, making an angle of 600 with the interface. (ang = 1.5
Solution
Angle of incidence (i) = 900 - 600 = 300
1.5 = sin 30°/sin r, sin r = sin 300/1.5 = 0.5/1.5
Sin r = 0.3333, sin-10.3333 = 19.50
R = 19.50