- Kinematics
- Dynamics
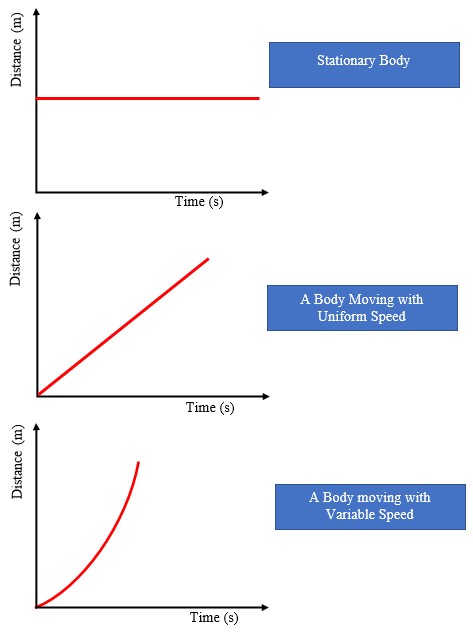
I. Displacement
- Distance moved by a body in a specified direction is called displacement. It is denoted by letter‘s’ and has both magnitude and direction. Distance is the movement from one point to another. The Si unit for displacement is the metre (m).II. Speed
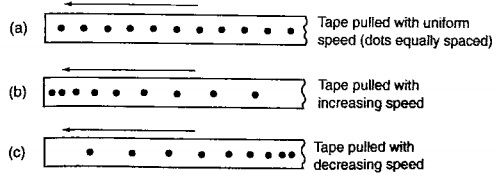
- This is the distance covered per unit time. Speed = distance covered / time taken. Distance is a scalar quantity since it has magnitude only. The SI unit for speed is metres per second (m/s or ms-1)Average speed = total distance covered / total time taken.
- Another unit for speed used is Km/h.
Example 1
A body covers a distance of 10m in 4 seconds. It rests for 10 seconds and finally covers a distance of 90m in 60 seconds. Calculate the average speed.
Solution
Total distance covered = 10 + 90 = 100m
Total time taken = 4 + 10 + 6 = 20 seconds
Therefore average speed = 100/20 = 5m/s
Example 2
Calculate the distance in metres covered by a body moving with a uniform speed of 180 km/h in 30 seconds.
Solution
Distance covered = speed × time
= 180 × 1000/60 × 60 = 50m/s
= 50 × 30
= 1,500m
Example 3
Calculate the time in seconds taken a by body moving with a uniform speed of 360km/h to cover a distance of 3,000 km?
Solution
Speed: 360 km/h = 360 × 1000/60 × 60=100m/s
Time = distance/speed
3000 × 1000/100
= 30,000 seconds.
III. Velocity
- This is the change of displacement per unit time. It is a vector quantity.Velocity=change in displacement/total time taken.
The SI units for velocity are m/s.
Example 4
A man runs 800m due North in 100 seconds, followed by 400m due South in 80 seconds. Calculate,
a. His average speed.
b. His average velocity.
c. His change in velocity for the whole journey
Solution
- Average speed: total distance travelled/total time taken.
= 800 + 400/100 + 80
= 1200/180
= 6.67m/s - Average velocity: total displacement/total time.
= 800 - 400/180
= 400/180
= 2.22 m/s due North
- Change in velocity=final-initial velocity
= (800/100) - (400-80)
= 8 - 5
= 3m/s due North
A tennis ball hits a vertical wall at a velocity of 10m/s and bounces off at the same velocity. Determine the change in velocity.
Solution
Initial velocity (u) = -10m/s
Final velocity (v) = 10m/s
Therefore change in velocity = v-u
= 10- (-10)
= 20m/s
IV. Acceleration
- This is the change of velocity per unit time. It is a vector quantity symbolized by ‘a’.Acceleration 'a' = change in velocity/time taken= v - u/t.
- The SI units for acceleration are m/s2.
Example 6
The velocity of a body increases from 72 km/h to 144 km/h in 10 seconds. Calculate its acceleration.
Solution
Initial velocity= 72 km/h = 20m/s
Final velocity= 144 km/h = 40m/s
Therefore 'a' = v - u/t
= 40 - 20/10
= 2m/s2
A car is brought to rest from 180km/h in 20 seconds. What is its retardation?
Solution
Initial velocity = 180km/h = 50m/s
Final velocity= 0 m/s
A = v - u/t = 0 - 50/20
= -2.5 m/s2
Hence retardation is 2.5 m/s2