Floating and Sinking - High School Physics Form 4

Archimedes, a Greek scientist carried out first experiments to measure upthrust on an object in liquid in the third century. Archimedes principle states that 'When a body is wholly or partially immersed in a fluid (liquid/ gas), it experiences an upthrust equal to the weight of the displaced fluid".

1. Pour water into an overflow can (eureka can) until it starts to flow out then wait until it stops dripping
2. Tie a suitable solid body securely and suspend it on a spring balance. Determine weight in air.
3. Lower the body slowly into the overflow can while still attached to the spring balance then read off its weight when fully submerged.
4. Weigh the displaced water collected in a beaker. Record your readings as follows

Weight of body in air = W₁
Weight of body in water = W₂
Weight of empty beaker = W₃
Weight of beaker and displaced liquid = W₄
Upthrust of the body = W1 – W₂
Weight of displaced water = W₄ – W₃

Discussion

The upthrust on the solid body will be found to be equal to the weight of displaced water therefore demonstrating the Archimedes principle.
Example
Solution
Volume of liquid displaced = 60 cm³ = 6.0 × 10-5 m³
Weight of the displaced liquid = volume × density × gravity = v × ρ × g
= 6.0 × 10^-5 × 1200 × 10
= 0.72 N
Upthrust = weight of the liquid displaced.
Weight of the block in the liquid = (4.80 – 0.72) = 4.08 N

Objects that float in a liquid are less dense than the liquid in which they float. We have to determine the relationship between the weight of the displaced liquid and the weight of the body.

Experiment: To demonstrate the law of floatation

Procedure

1. Weigh the block in air and record its weight as W1.
2. Put water into the overflow can (eureka can) up to the level of the spout.
3. Collect displaced water in a beaker. Record the weight of the beaker first in air and record as W2. Weigh both the beaker and the displaced water and record as W3.
4. Record the same procedure with kerosene and record your results as shown below.



5. What do you notice between W₁ and W₃ – W₂

Discussion

The weight of the displaced liquid is equal to the weight of the block in air. This is consistent with the law of floatation which states that "A body displaces its own weight of the liquid in which it floats". Mathematically, the following relation can be deduced Weight = volume × density × gravity = v × ρ × g, therefore W = v d × ρ × g where v is the volume of displaced liquid.

NOTE – Floatation is a special case of Archimedes principle. This is because a floating body sinks until the upthrust equals the weight of the body.

Example
Solution
Volume of the spirit displaced = (3 × 3 × 4) = 36 cm3 = 3.6 × 10-5 m³ Weight of the block =v d × ρ × g = (3.6 × 10^-5) × 8.0 × 102× 10 = 2.88 × 10^-1 N.

We have established the relative density as the ratio of the density of a substance to the density of water. Since by the law of floatation an object displaces a fluid equal to its own weight hence the following mathematical expressions can be established.
Relative density = density of substance / density of water.
= weight of substance / weight of equal volume of water
= mass of substance / mass of equal volume of water

Applying Archimedes principle, the relative density'd';

d = weight of substance in air / upthrust in water or d = W / u Since upthrust is given by (W2 - W1)where W2 – weight in air, W2– weight when submerged.
Hence d = W / u = W / W2 – W1, the actual density, ρ of an object can be obtained as follows ρ of an object = d × 1,000 kgm^-3

Experiment:To determine the relative density of a cork

Procedure

1. Select a sinker which is heavy enough to make the cork to sink.
2. Attach the cork and the sinker as follows
3. Record the results obtained as follows

Weight of the sinker in water = W1
Weight of the sinker in water and cork in air = W2
Weight of the sinker and cork in water = W3
Weight of the cork in air = W2 – W1
Upthrust on the cork = W2 – W3
The relative density of the cork in air is determined as follows;
d = weight of the cork in air / upthrust on the cork.

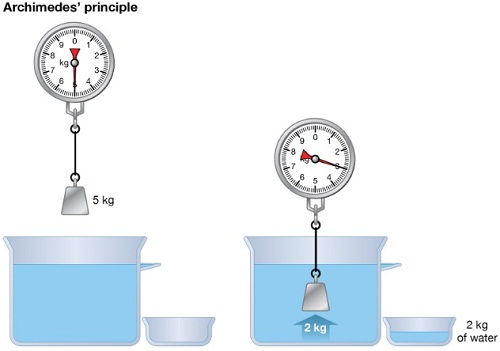
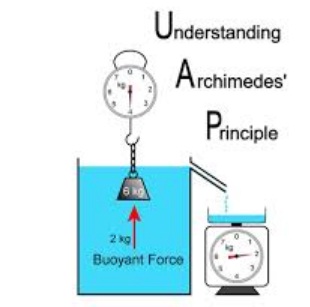
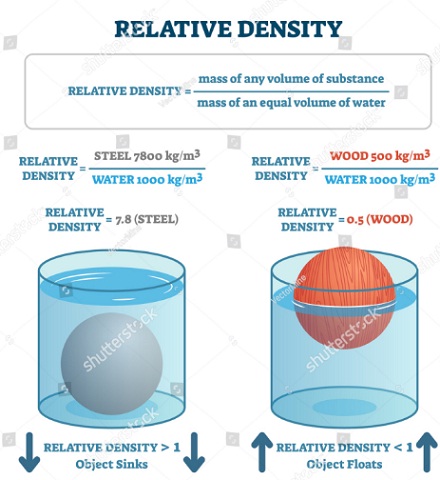
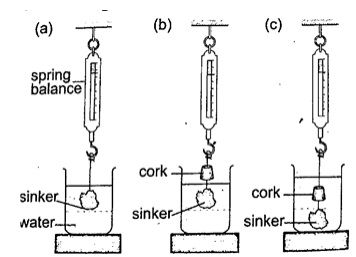
1. Ships

steel which is used to make ships is 6-7 times dense than water but a ship is able to float on water because it is designed to displace more water than its volume. Load lines called Plimsoll marks are marked on the side to indicate the maximum load at different seasons to avoid overloading.

2. Submarines

they are made of steel and consists of ballast tanks which contain water when theyhave to sink and filled with air when they have to float. This makes the submarines to balance their weight and be able to rise upwards.

3. Balloons

when they are filled with helium gas balloons become lighter and the upthrust on the balloon becomes greater than their weight therefore becoming able to rise upwards.

4. Hydrometers

they are used to measure the relative densities of liquids quickly and conveniently. Various types of hydrometers are made to measure different ranges of different densities i.e. lactometer – for measuring milk water (range 1.015 – 1.045), battery acid tester – used to test the charge in a lead-acid battery.

Examples

Solution
Mass of solid = 1.0 kg
Weight of solid W = mg = 10 N
Tension on the string (T) = 5 N
Upthrust on solid (u) = W – T = 10 – 5 = 5
Relative density (d) = W / u = 10 / 5 = 2.

Solution
Upthrust = weight of the air displaced
= volume of air × density × gravity
= (1.0 × 107 × 106 ) × (1.25 × 10)
= 10 × 1.25 × 10 = 125 N
Weight of hydrogen = 10 × 0.09 × 10 = 9 N
Total weight of hydrogen and fabric = 80 + 9 = 89 N
Total additional weight to be lifted = 125 – 89 = 36 N.

Solution
Let the volume of the material be V cm³
The mass of the material be 8.5 V grams
Volume of wood = 100 g / 0.2 g/cm = 500 cm³
In order to have an average density of 1.2 gcm^-3
= total mass / total volume
Therefore (100 + 8.5V) / (500 + V) = 1.2 gcm^-3
Hence V = 68.5 cm³