Equilibrium and Centre of Gravity | High School Physics Form 2

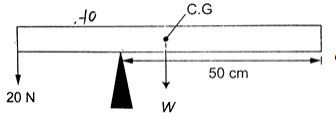
- For a body to be in equilibrium (neither moving nor rotating), under the action of parallel forces, the following conditions will be satisfied;

1. The sum of upward forces must be equal to the sum of downward forces.
2. The sum of clockwise moments equals the sum of anticlockwise moments.

- The two are called the first and second condition of equilibrium respectively.

Practice Example 1

1. A uniform rod of length 1.0 m is hung from a spring balance as shown and balanced in horizontal position by a force of 1.6 N. Determine:
a) The weight of the rod.
b) Reading of the spring balance.

Solution

a) Let the weight of the rod be 'W'. W acts at 50 cm mark, therefore taking moments about point of suspension, clockwise moments = W x 0.2 Nm = 0.2W Nm.
Anticlockwise moments = 1.6 x 0.3 = 0.48 Nm.
Using the law of moments, then
Anticlockwise moments = clockwise moments
0.48 = 0.2 W, hence W = 2.4 N

b) Upward forces = downward forces
Downward force = W + 1.6 N
= 2.4 + 1.6 = 4.0 N
Upward force = reading of the spring balance = 4.0 N

Practice Example 2

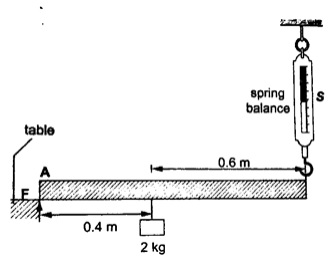
2. A uniform rod is 1.0 m long weighs 5 N. It is supported horizontally at one end by a spring and the other end rests on a table as shown below. A mass of 2 kg is hung from the rod as shown; determine:
a) Reading of the spring balance
b) Reaction force, F, from the table.

Solution

a) The 2kg mass and the weight of the rod (5 N) gives clockwise moment while the spring balance provides anticlockwise moments.
Clockwise moments = (2 x 10) x 0.4 + (5 x 0.5) = 10.5 Nm.
Anticlockwise moments = S x 1 (reading of the spring balance)
1S = 10.5, hence S = 10.5 N.

b) Upward forces = downward forces.
Downward forces = (2 x 10) + 5 = 25 N.
Therefore F + 10.5 = 25, hence F = 14.5 N.

-This is a term which explains how easy or difficult it is for an object to topple over when a force is applied to it.

Factors affecting stability

1. Base area – the bigger the base area the more the stability.
2. Position of the centre of gravity – the higher the centre of gravity the less stable the body will be.

States of equilibrium.

1. Stable equilibrium – if a body is displaced by a small amount of force it returns to its original position.
2. Unstable equilibrium – if a body is displaced by a small amount of force it toppled over and does not return to its original position.
3. Neutral equilibrium – a body is at rest in whichever position it is placed in i.e. it does not rise or fall when displaced.

State of Equilibrium

Applications of Stability

It is used mainly in the design of motor vehicles i.e.

1. Racing cars – they have a low and wide wheelbase to increase their base area.
2. Double decker buses – they are manufactured with a low centre of gravity by mounting their chassis and engines as low as possible.