Energy, Work, Power And Machines - High School Physics Form 3

This is the ability to do work.

Forms of energy

a. Chemical energy: - this is found in foods, oils charcoal firewood etc.
b. Mechanical energy: - there are four types;

1. Potential energy – a body possesses potential energy due to its relative position or state
2. Kinetic energy – energy possessed by a body due to its motion i.e. wind, water
3. Wave energy – wave energy may be produced by vibrating objects or particles i.e. light, sound or tidal waves.
4. Electrical energy – this is energy formed by conversion of other forms of energy i.e. generators.

Transformation and conservation of energy

- Any device that facilitates energy transformations is called transducer.
- The law of conservation of energy states that energy cannot be created or destroyed; it can only be transformed from one form to another.

Work

Work is done when a force acts on a body and the body moves in the direction of the force.
Work done = force × distance moved by object.
W = F × d
Work is measured in Nm. 1 Nm = 1 Joule (J)

Example 1
Calculate the work done by a stone mason lifting a stone of mass 15 kg through a height of 2.0 m. (take g=10N/kg)
Solution

Work done = force × distance
= (15 × 10) × 2 = 300 Nm or 300 J

---

Example 2
A girl of mass 50 kg walks up a flight of 12 steps. If each step is 30 cm high, calculate the work done by the girl climbing the stairs.
Solution

Work done = force × distance
= (50 × 10) × (12 × 30) ÷ 100 = 500 × 3.6 = 1,800 J

---

Example 3
A force of 7.5 N stretches a certain spring by 5 cm. How much work is done in stretching this spring by 8.0 cm?
Solution

A force of 7.5 produces an extension of 5.0 cm.
Hence 8.0 cm = (7.5 × 8)/ 5 = 12.0 N
Work done = ½ × force × extension
= ½ × 12.0 × 0.08 = 0.48 J

---

Example 4
A car travelling at a speed of 72 km/h is uniformly retarded by an application of brakes and comes to rest after 8 seconds. If the car with its occupants has a mass of 1,250 kg. Calculate;
a) The breaking force
b) The work done in bringing it to rest
Solution

a) F = ma and a = v – u/t
But 72 km/h = 20m/
a = 0 - 20/8 = - 2.5 m/s
Retardation = 2.5 m/s
Braking force F = 1,250 × 2.5
= 3,125 N

b) Work done = kinetic energy lost by the car
= ½ mv² – ½ mu²
= ½ × 1250 × 0
2 – ½ × 1250 × 20²
= - 2.5 × 10⁵J

---

Example 5
A spring constant k = 100 Nm is stretched to a distance of 20 cm. calculate the work done by the spring
Solution

Solution
Work = ½ ks²
= ½ × 100 × 0.2²
= 2 J

---

Power

Power is the time rate of doing work or the rate of energy conversion.
Power (P) = work done / time
P = W / t
The SI unit for power is the watt (W) or joules per second (J/s).

Example 6
A person weighing 500 N takes 4 seconds to climb upstairs to a height of 3.0 m. what is the average power in climbing up the height?
Solution

Power = work done / time = (force × distance) / time
= (500 × 3) / 4 = 375 W

---

Example 7
A box of mass 500 kg is dragged along a level ground at a speed of 12 m/s. If the force of friction between the box and floor is 1200 N. Calculate the power developed
Solution

Power = Fv
= 2,000 × 12
= 24,000 W = 24 kW.

Machine

A machine is any device that uses a force applied at one point to overcome a force at another point.
Force applied is called the effort while the resisting force overcome is called load.
Machines makes work easier or convenient to be done. Three quantities dealing with machines are;-

1. Mechanical advantage (M.A.) - this is defined as the ratio of the load (L) to the effort (E). It has no units.
   M.A = load (L) / effort (E)
2. Velocity ratio – this is the ratio of the distance moved by the effort to the distance moved by the load.
   V.R = distance moved by effort/ distance moved by the load.
3. Efficiency – is obtained by dividing the work output by the work input and the getting percentage
   Efficiency = (work output/work input) × 100
   = (M.A / V.R) × 100
   = (work done on load / work done on effort) × 100

---

Example 8
A machine; the load moves 2 m when the effort moves 8 m. If an effort of 20 N is used to raise a load of 60 N, what is the efficiency of the machine?
Solution

Efficiency = (M.A / V.R) × 100 M.A = load/effort = 60/20 = 3
V.R = DE/ DL = 8/2 = 4
Efficiency = ¾ × 100 = 75%
Some simple machines

a) Levers

– this is a simple machine whose operation relies on the principle of moments.

b) Pulleys

– this is a wheel with a grooved rim used for lifting heavy loads to high levels.
The can be used as a single fixed pulley, or as a block-and-tackle system.

M.A = Load/ Effort
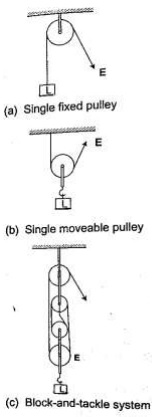
V.R = no. of pulleys/ no. of strings supporting the load



Example 9
A block and tackle system has 3 pulleys in the upper fixed block and two in the lower moveable block. What load can be lifted by an effort of 200 N if the efficiency of the machine is 60%?
Solution

V.R = total number of pulleys = 5
Efficiency = (M.A/V.R) × 100 = 60%
0.6 = M.A/5 = 3, but M.A = Load/Effort
Therefore, load = 3 × 200 = 600 N

c) Wheel and Axle

– consists of a large wheel of big radius attached to an axle of smaller radius.

V.R = R/r and M.A = R/r
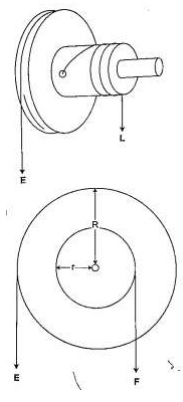
Example 10
A wheel and axle is used to raise a load of 280 N by a force of 40 N applied to the rim of the wheel. If the radii of the wheel and axle are 70 cm and 5 cm respectively. Calculate the M.A, V.R and efficiency.
Solution

M.A = 280 / 40 = 7
V.R = R/r = 70/5 = 14
Efficiency = (M.A/V.R) × 100 = 7/14 × 100 = 50 %

---

d) Inclined plane

V.R = 1/ sin Θ
M.A = Load/ Effort
Example 11
A man uses an inclined plane to lift a 50 kg load through a vertical height of 4.0 m. the inclined plane makes an angle of 300 with the horizontal. If the efficiency of the inclined plane is 72%, calculate;
a) The effort needed to move the load up the inclined plane at a constant velocity.
b) The work done against friction in raising the load through the height of 4.0 m. (take g= 10 N/kg)
Solution

a) V.R = 1 / sin C = 1/ sin 300 = 2 M.A = efficiency × V.R = (72/100)× 2 = 1.44
Effort = load (mg) / effort (50 × 10)/ 1.44 = 347.2 N

b) Work done against friction = work input – work output
Work output = m g h = 50 × 10 × 4 = 2,000 J
Work input = effort × distance moved by effort
347.2 × (4 × sin 300) = 2,777.6 J
Therefore work done against friction = 2,777.6 – 2,000 = 777.6 J

---

e) The screw:

- the distance between two successive threads is called the pitch
V.R of screw = circumference of screw head / pitch P
= 2πr / P

Example 12
A car weighing 1,600 kg is lifted with a jack-screw of 11 mm pitch. If the handle is 28 cm from the screw, find the force applied.
Solution

Neglecting friction M.A = V.R
V.R = 2Πr /P = M.A = L / E
1,600 / E = (2Π × 0.28) / 0.011
E = (1,600 × 0.011 × 7) / 22 × 2 × 0.28 =10 N

---

f) Gears:

- the wheel in which effort is applied is called the driver while the load wheel is
V.R = revolutions of driver wheel / revolutions of driven
Or
V.R = no. of teeth in the driven wheel/ no. of teeth in the driving wheel

g) Pulley belts:

-these are used in bicycles and other industrial machines
V.R = radius of the driven pulley / radius of the driving pulley

h) Hydraulic machines

V.R = R²/ r² where R- radius of the load piston and r- radius of the effort piston

Example 13
The radius of the effort piston of a hydraulic lift is 1.4 cm while that of the load piston is 7.0 cm. This machine is used to raise a load of 120 kg at a constant velocity through a height of 2.5 cm. given that the machine is 80% efficient, calculate;
a) The effort needed
b) The energy wasted using the machine
Solution

a) V.R = R²/ r² = (7 × 7) / 1.4 × 1.4 = 25
Efficiency = M.A / V.R = (80 /100) × 25 = 20
But M.A = Load / Effort = (120 × 10) / 20 = 60 N

b) Efficiency = work output / work input = work done on load (m g h) /80
= (120 × 10 × 2.5) / work input
80 / 100 = 3,000 / work input
Work input = (3,000 × 100) /80 = 3,750 J
Energy wasted = work input – work output
= 3,750 – 3,000 = 750 J