Electrostatics II - High School Physics Form 3

- An electric field is the space around a charged body where another charged body would be acted on by a force. These fields are represented by lines of force.
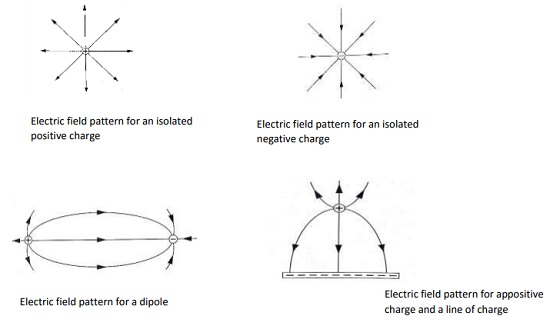
-This line of force also called an electric flux line points in the direction of the force.

Electric field patterns

- Just like in magnetic fields, the closeness of the electric field-lines of force is the measure of the field strength.
- Their direction is always from the north or positive to the south or negative.

Charge distribution on conductors’ surface

- A proof plane is used to determine charge distribution on spherical or pear-shaped conductors.
- For an isolated sphere it is found that the effect is the same for all points on the surface meaning that the charge is evenly distributed on all points on the spherical surface.

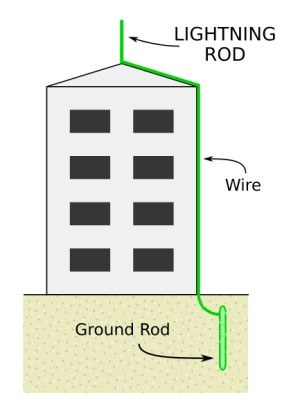
The lightning arrestors

- Lightning is a huge discharge where a large amount of charge rushes to meet the opposite charge.
- It can occur between clouds or the cloud and the earth. Lightning may not be prevented but protection from its destruction may be done through arrestors.
- An arrestor consists of a thick copper strip fixed to the outside wall of a building with sharp spikes.

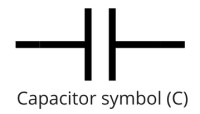
Capacitors and Capacitance

- A capacitor is a device used for storing charge. It consists of two or more plates separated by either a vacuum or air.
- The insulating material is called dielectric. They are symbolized as shown below,

Capacitance C = Q / V where Q is charge and V is voltage.
The units for capacitance are coulombs per volt (Coul /volt) and are called farads.
1 Coul/ volt = 1 farad (F)
1 µF = 10^-6F and 1pF = 10^-12

Types of capacitors are;

• Paper capacitors
• Electrolyte capacitors
• Variable capacitors
• Plastic capacitors
• Ceramic capacitors
• Mica capacitors

Factors affecting the capacitance of a parallel-plate capacitor

1. Distance between the plates: - reducing separation increases capacitance but the plates should not be very close to avoid ionization which may lead to discharge.
2. Area of plate: - reduction of the effective area leads to reduction in capacitance.
3. Dielectric material between plates: - different materials will produce different capacitance effects.

Charging and discharging a capacitor

- When the switch S¹ is closed the capacitor charges through resistor R and discharges through the same resistor when switch S² is closed.

Applications of capacitors

• Variable capacitor: - used in tuning radios to enable it transmit in different frequencies.
• Paper capacitors: - used in mains supply and high voltage installations.
• Electrolytic capacitors: - used in transistor circuits where large capacitance values are required.

Example 1
A capacitor of two parallel plates separated by air has a capacitance of 15pF. A potential difference of 24 volts is applied across the plates,
a) Determine the charge on the capacitors.
b) When the space is filled with mica, the capacitance increases to 250pF. How much more charge can be put on the capacitor using a 24 V supply?
Solution

a) C= Q / V then Q = VC, hence Q = (1.5 × 10^-12) × 24 = 3.6 × 10^-10 Coul.

b) Mica C = 250pF, Q = (250 × 10^-12) × 24 = 6 × 10^-9 Coul.
Additional charge = (6 × 10^-9) – (3.6 × 10^-10) = 5.64 × 10^-9 Coul.

---

Capacitor combination

1. Parallel combination – for capacitors in parallel the total capacitance is the sum of all the separate capacitances.
C_T = C₁ + C₂ + C₃ + .....

2. Series combination – for capacitors in series, the reciprocal of the total capacitance is equal to the sum of the reciprocals of all the separate capacitances.
1/ C_T = 1 / C₁ + 1 / C₂ + 1 / C₃
For two capacitors in series then total capacitance becomes,
CT = (C₁ C₂) / (C₁ + C₂)

Example 2
Three capacitors of capacitance 1.5µF, 2micro;F and 3micro;F are connected to a potential difference of 12 V as shown.

Find;
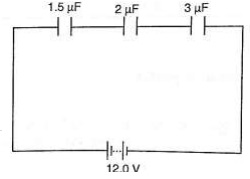
a) The combined capacitance
b) The charge on each capacitor
c) The voltage across the 2 µF capacitor
Solution

a) 1 /C_T = 1/ 1.5 + 1 / 3.0 + 1 /20 = 3/2 hence C_T = 0.67 µF
b) Total charge, Q = V C , (2/3 × 10^-6) × 12.0 V = 8 × 10^-6 = 8 µC.
c) The charge is the same for each capacitor because they're in series hence = 8 µC.
d) V = Q / C, then V = 8 µC / 2 µF = 4 V.

---

Example 3
Three capacitors of capacitance 3 µF, 4 µF and 5 µF are arranged as shown. Find the effective capacitance.

Solution

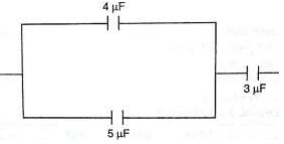
Since 4 µF and 5 µF are in parallel then, CT = 9 µF,
then the 9 µF is in series with 3 µF,
Hence CT = 27/12 = 2.25 µF

---

Example 4
Calculate the charges on the capacitors shown below

Solution

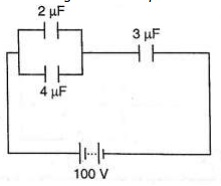
The 2 µF and 4 µF are in parallel then combined capacitance = 6 µF
The 6 µF is in series with the 3 µF capacitor hence combined capacitance = 18 / 9 = 2 µF
Total charge Q = CV then Q = (2.0 × 10^-6) × 100 = 2.0 × 10^-4 C
The charge on the 3 µF capacitor is also equal to 2.0 × 10^-4 C
The p.d across the 3 µF capacitor => V = Q / C => (2.0 × 10^-4)/ 3.0 × 10⁶
= 2/3 × 10² = 66.7 V
The p.d across the 2 µF and 4 µF is equal to 100 V – 66.7 V = 33.3 V,
Hence Q1 = CV = 2.0 × 10^-6 × 33.3 = 6.66 × 10^-5 C
Q2 = CV = 4.0 × 10^-6 × 33.3 = 1.332 × 10^-4 C

---

N.B
Energy stored in a capacitor is calculated as;
Work done (W) = average charge × potential difference
W = ½QV or ½CV²

Example 6
A 2 µF capacitor is charged to a potential difference of 120 V. Find the energy stored in it.
Solution

W = ½CV² = ½× 2 × 10^-6 × 120² = 1.44 × 10^-2J