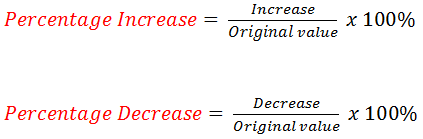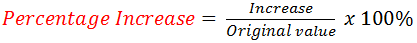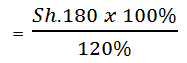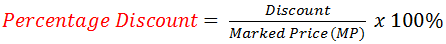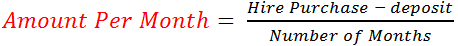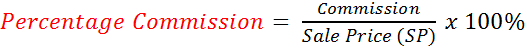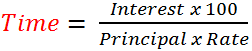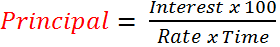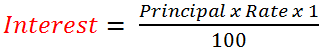Key Formulae:
Hire Purchase (H.P) = Deposit + Total Monthly Instalments
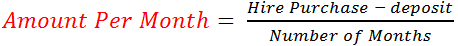
Cash Price (CP) is ALWAYS 100%
Example 1
In a certain shop, the hire purchase terms of a new bicycle is a deposit of sh. 12,500 and 15 monthly instalments of sh. 7,500 each. This is 25% more than the cash price. What is the cash price of the bicycle.
Solution:
Total Monthly Instalments = sh. 7,500 x 15 = sh. 112,500
Hire Purchase Price (HPP) = Deposit + Total Monthly Instalments
= sh. 12,500 + sh. 112,5000
= sh. 125,000
CP = 100%
HPP = 100% + 25% = 125%
If:
125% = sh. 112,500
100% = sh. ?
= (100% x sh. 125, 000) / 125%
CP = sh. 100,000
Example 2
The cash price of a microwave is sh. 18,000. The hire purchase price of the microwave is 20% more than the cash price. Bernice bought it on hire purchase terms by paying 40% of the hire purchase price as the deposit and the balance equal monthly instalments of sh. 1,620. How many instalments did she pay?
Solution:
Remember that the Cash Price (CP) = 100%
Hire purchase = 100% + 20% = 120% of the cash price
Hence:
HP = (120 / 100) x 18,000 = sh. 21,600
Deposit: 40% of the HP
D = (40/100) x 21600 = sh. 8,640
Number of Months = (Hire Purchase (HP) - Deposit(D)) / Monthly instalments (MI)
= (21,600 - 8,640) / 1,620 = 8 Months