The Gas Laws - High School Physics Form 3

- This law states that "the pressure of a fixed mass of a gas is directly proportional to the absolute temperature if the volume is kept constant". The comparison between Kelvin scale and degrees Celsius is given by;
θ0 = (273 + θ) K, and T (K) = (T – 273) °C.

Example 1
A gas in a fixed volume container has a pressure of 1.6 × 10⁵ Pa at a temperature of 27°C. What will be the pressure of the gas if the container is heated to a temperature of 277 °C?
Solution

Since law applies for Kelvin scale, convert the temperature to kelvin
T1 = 27 °C = (273 + 27) K = 300 K
T2 = 227 °C = (273 + 277) = 550 K
P₁ / T₁ = P₂ / T₂, therefore P₂ = (1.6 × 10⁵) × 550 / 300 = 2.93 × 10⁵ Pa.

Example 2
At 20 °C, the pressure of a gas is 50 cm of mercury. At what temperature would the pressure of the gas fall to 10 cm of mercury?
Solution

P / T = constant, P₁ / T₁ = P₂ / T₂, therefore T₂ = (293 × 10) / 50 = 58.6 K or (– 214.4 °C.

Charles law

Charles law states that "the volume of a fixed mass of a gas is directly proportional to its absolute temperature (Kelvin) provided the pressure is kept constant". Mathematically expressed as follows,
V₁ / T₁ = V₂ / T₂

Example 3
A gas has a volume of 20 cm³ at 27 °C and normal atmospheric pressure. Calculate the new volume of the gas if it is heated to 54 °C at the same pressure.
Solution

Using, V₁ / T₁ = V₂ / T₂, then V₂ = (20 × 327) / 300 = 21.8 cm³.

---

Example 4
0.02m³ of a gas is at 27 °C is heated at a constant pressure until the volume is 0.03 m³. Calculate the final temperature of the gas in °C.
Solution

Since V₁ / T₁ = V₂ / T₂, T² = (300 × 0.03) / 0.02 = 450 K or 177 °C

---

Boyle's law

Boyle's law states that the pressure of a fixed mass of a gas is inversely proportional to its volume provided the temperature of the gas is kept constant. Mathematically expressed as,
P₁ V₁ = P₂ V₂

Example 5
A gas in a cylinder occupies a volume of 465 ml when at a pressure equivalent to 725 mm of mercury. If the temperature is held constant, what will be the volume of the gas when the pressure on it is raised to 825 mm of mercury?
Solution

Using, P₁ V₁ = P₂ V₂, then V₂ = (725 × 465) / 825 = 409 ml.

---

Example 6
The volume of air 26 cm long is trapped by a mercury thread 5 cm long as shown below. When the tube is inverted, the air column becomes 30 cm long. What is the value of atmospheric pressure?

Solution

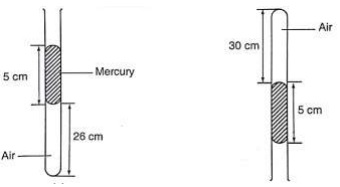
Before inversion, gas pressure = atm. Pressure + h p g
After inversion, gas pressure = atm. Pressure - h p g
From Boyle's law, P1 V1 = P2 V2, then let the atm. Pressure be ‘x',
So (x + 5) 0.26 = (x – 5) 0.30
0.26x + 1.30 = 0.3x - 1.5, x = 2.8/ 0.04 = 70 cm.

---

A general gas law

Any two of the three gas laws can be used derive a general gas law as follows,
P₁ V₁ / T₁ = P₂ V₂ / T₂ or
P V / T = constant – equation of state for an ideal gas.

Example 7
A fixed mass of gas occupies 1.0 × 10-3 m³ at a pressure of 75 cmHg. What volume does the gas occupy at 17.0 °C if its pressure is 72 cm of mercury?
Solution

P V / T = constant so V₁ = (76 × 1.0 × 10^-3 × 290) / 273 × 72 = 1.12 × 10³ m³.

---

Example 8
A mass of 1,200 cm³ of oxygen at 27 °C and a pressure 1.2 atmosphere is compressed until its volume is 600 cm³ and its pressure is 3.0 atmosphere. What is the Celsius temperature of the gas after compression?
Solution

Since P₁ V₁ / T₁ = P₂ V₂ / T₂, then T₂ = (3 × 600 × 300) / 1.2 × 1,200 = 375 K or 102 °C.