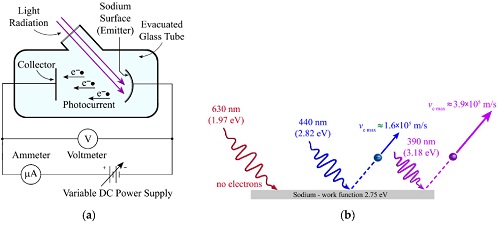
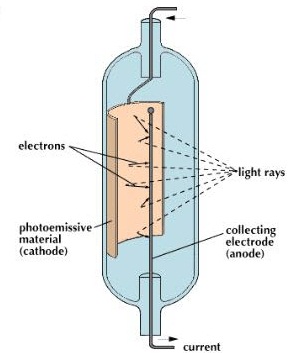
As an electron escapes, energy equivalent to the work function of the emitter substance is 'given up'.
So the
photon energy must be greater than or equal to Φ. If the ‘h f' is greater than Φ then the
electron acquires some kinetic energy after leaving the surface. The maximum kinetic energy of the
ejected photoelectron is given by;
K.E max = ½ m v2
max = h f – Φ ………………(i), where m v2
max = maximum velocity and mass.
This is the Einstein's photoelectric equation.
If the photon energy is just equivalent to work function then, m v2
max = 0, at this juncture the electron
will not be able to move hence no photoelectric current, giving rise to a condition known as cut-off
frequency, h fco = Φ………………. (ii)
Also the p.d required to stop the fastest photoelectron is the cut-off potential, V cowhich is given by E = e V co electron volts, but this energy is the maximum kinetic energy of the photoelectrons and therefore,
½ m v2
max = e V co ………….. (iii).
Combining equations (i), (ii) and (iii), we can write Einstein's photoelectric equation as,
e V co = h f – h fco ………………….. (iv)
NOTE: -- Equations (i) and (iv) are quite useful in solving problems involving photoelectric effect.
Examples
1. The cut-off wavelength for a certain material is 3.310 × 10-7 m. What is the cut-off frequency for
the material?
Solution
Speed of light ‘c' = 3.0 × 108 m/s. Since f = c / λ, then
f = 3.0 × 108/ 3.310 × 10
-7
= 9.06 × 1014 Hz.
2. The work function of tungsten is 4.52 e V. Find the cut-off potential for photoelectrons when a
tungsten surface is illuminated with radiation of wavelength 2.50 × 10-7 m. (Planck's constant, h
= 6.62 × 10-34 Js).
Solution
Frequency ‘f' = c / λ = 3.0 × 108/ 2.50 × 10
-7
Energy of photon = h f = 6.62 × 10
-34 × (3.0 × 108/ 2.50 × 10
-7) × (1 / 1.6 × 10
-19)
= 4.97 eV.
Hence h fco = 4.52 e V. e V co = 4.97 e V - 4.52 e V = 0.45 e V = 7.2 × 10
-20 J
V co = 7.2 × 10-20 / 1.6 × 10
-19 = 0.45 e V.
3. The threshold frequency for lithium is 5.5 × 1014 Hz. Calculate the work function for lithium. (Take
‘h' = 6.626 × 10-34 Js)
Solution
Threshold frequency, f o = 5.5 × 1014 Hz, ‘h' = 6.626 × 10
-34 Js
Φ = h f = 5.5 × 1014× 6.626 × 10
-34 = 36.4 × 10
-20
4. Sodium has a work function of 2.0 e V. Calculate
a) The maximum energy and velocity of the emitted electrons when sodium is
Illuminated by a radiation of wavelength 150 nm.
b) Determine the least frequency of radiation by which electrons are emitted.
(Take ‘h' = 6.626 × 10-34 Js, e = 1.6 × 10-19, c = 3.0 × 108 m/s and mass of electron
= 9.1 × 10-31 kg).
Solution
a) The energy of incident photon is given by h f = c / λ
= (6.626 × 10
-34 × 3.0 × 108) / 1.50 × 10
-9
= 1.325 × 10
-18 J