Esoma-KE Logo
esoma@esomake.co.ke
Change Class  |  Change Subject

Hooke's law | High School Physics Form 2

  Change Class FORM ONE
Select Subject  |  Physics

PHYSICS REVISION QUESTIONS

Click to Attempt Form 2 Physics Questions




Want to enjoy learning? Try reading without Ads!

Say goodbye to distractions and enjoy uninterrupted learning with our new ad-free feature. Dive into our vast collection of educational content without any interruptions.

Explore Ad-Free learning plus lots of other premium benefits for as little as KES 500 per month.
Click to Join Now→


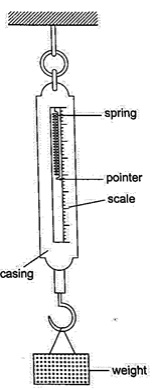
Hooke's Law: Introduction

- Hooke's law states that the extension of a spring is proportional to the applied force, provided that the force is not large enough to deform the spring permanently.
- Mathematically expressed as Force α extension.

Spring Constant

- Since Force α extension then Force / Extension = constant (k).
- The constant of proportionality (k) is called the spring constant.
F / e = k or Force (N) = k e.
- The spring constant is a measure of the stiffness of a spring. The greater the constant the stiffer the spring.
- The spring constant varies with the following;
  1. Material – identical springs mad of different materials will have different constants i.e. steel and copper.
  2. Diameter – the stiffness decreases with the increase in diameter.
  3. Thickness of the wire – a spring made of a thicker wire is stiffer than the one made of thin wire of the same material.
  4. Length of spring – a short spring is stiffer than a longer one.
  5. Number of turns per unit length – a spring with higher number of turns per unit length is less stiff than the one with fewer turns per unit length.


Practice Example 1

1. If the springs shown below are similar and the constant of proportionality (k) is 100 Nm-1, determine total extension in each arrangement.

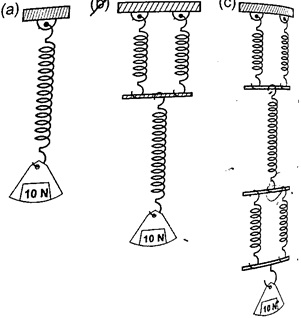
Hooke's Law Example - Physics Form Two

Solution
k = 100 Nm-1
extension = force / k = 10 ÷ 100 = 0.1 m = 10 cm. Extension of the lower spring = 10 cm, extension of the two parallel springs = 5 cm.
Total extension = 10 + 5 = 15 cm. Extension of the two lower springs = 5 cm
Middle spring extend by = 10 cm
Upper two springs extend by = 5 cm
Total extension = 5 + 10 + 5 = 20 cm.


The spring balance

- It is made up of a spring mounted in a metal or plastic casing.
- The spring is fitted with a pointer which moves along a calibrated scale divided into ten equal parts.

Hooke's Law Example - Physics Form Two


Practice Example 1

1. A load of 4 N causes a certain copper wire to extend by 1.0 mm. Find the load that will cause a 3.2 mm extension on the same wire. (Assume Hooke's law is obeyed).
Solution
F α e, also F1 / F2 = e1 / e2
= F2 = (4 × 3.2) / 1.0
= 12.8 N.

Practice Example 2

2. A body of 200 g was hung from the lower end of a spring which obeys Hooke's law. Given that the spring extended by 100 mm, what is the spring constant for this spring?
Solution
F = α e, F = k e. F = 200 x 10-3
kg x 10 N /kg = 2 N.
Extension = 100 x 10-3 m = 0.1 m.
Spring constant (k) = 2 / 0.1 = 20 N/m.

Practice Example 3

3. Two identical springs, whose spring constant is 6.0 N/cm, are used to support a load of 60 N as shown below. Determine the extension of each spring.

Hooke's Law Example - Physics Form Two

Solution
Since the springs are parallel their spring constant equals 2k.
Therefore extension = Force / k = 2 F / k = 60 / 2 x 6 = 5 cm.
Each spring will extend by 5 cm.


Hello Esoma-KE Member, please help review these notes.    Why review


Very Poor Poor Good

Very Good Excellent
Your review has been successfully submitted.
Tell us what you think about the notes.

Submit Comment

Students' and Teachers' Reviews


Here's what our users had to say ...

Guest User
It is very understandable