Esoma-KE Logo
esoma@esomake.co.ke
Change Class  |  Change Subject

Quadratic Expressions And Equations I

  Change Class FORM ONE
Select Subject  |  Mathematics

MATHEMATICS REVISION QUESTIONS

Click to Attempt Form 2 Mathematics Questions




Want to enjoy learning? Try reading without Ads!

Say goodbye to distractions and enjoy uninterrupted learning with our new ad-free feature. Dive into our vast collection of educational content without any interruptions.

Explore Ad-Free learning plus lots of other premium benefits for as little as KES 500 per month.
Click to Join Now→


Expansion of Algebraic Expressions

Earlier, you read that:

a(b + c) = ab + ac

Example 1
Expand (2x - 3)(3x + 4)

= 2x(3x + 4) - 3(3x + 4)
= 6x2 + 8x - 9x -12
= 6x2 - x - 12

Quadratic Identities

They are represented as:

1. (a + b)(a + b)
2. (a - b)(a - b)
3. (a + b)(a - b)

Example 2
Consider the third identity Expand (a + b)(a - b)

= a(a - b) + b(a - b)
= a2 - ab + ba - b2
= a2 - b2

This is referred to as the difference of two squares.


Example 3
Using Quadratic identity Expand (3x + 4)(3x - 4)

From difference of two squares:
(a + b)(a - b) = a2 - b2
= (3x)2 - 42
= 9x2 - 16



Factorization of quadratic expressions

- This is the opposite of expansion (explained above).

While a(b + c) = ab + ac is expansion
ab + ac = ab + ac is factorization

Example 4
Factorize 3x2 - 9x

3x is common hence:
= 3x(x - 3)


Example 5
Factorize x2 + 7x + 12

Use the rule: ax2 + bx + c
p x q = c and p + q = b
p x q = 12 and p + q = 7
The numbers are 4 and 3 since 4 x 3 = 12 and 4 + 3 = 7
x2 + 3x + 4x + 12
= x(x + 3) + 4(x + 3)
= (x + 4)(x + 3)




Solving Quadratic Equations By Factorization

- If a x b = 0, either a = 0 or b = 0.
Example 6
Solve the equation 2x2 + 7x + 6 = 0

2x2 + 7x + 6 = 0
2x2 + 3x + 4x + 6 = 0
x(2x+3) + 2(2x + 3) = 0
(2x + 3)(x + 2) = 0
First Part:
2x + 3 = 0
2x = -3
x = -3/2
Second Part:
x + 2 = 0
x = -2

Hence x = -2 and x = -3/2


Sum and product of roots of an equation

The solution obtained in solving quadratic equations may also be termed as roots or a quadratic equation.
Note:

Hence:

Example 7
Given that the roots of the equation 3x2 - 4x - 4 = 0 are a and b find 1/a + 1/b


Formation of a quadratic equation

Given the roots an equation, a quadratic equation can be formed.
Note:
Example 8
Form the quadratic equation whose roots are:
1/2 or 2/3

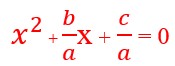
x = ½ or x = 2/3
2x = 1 or 3x = 2
2x - 1 = 0 or 3x - 2 = 0
(2x - 1)(3x - 2) = 0
2x(3x - 2) - 1(3x - 2) = 0
6x2 - 4x - 3x + 2 = 0
6x2 - 7x + 2 = 0




Hello Esoma-KE Member, please help review these notes.    Why review


Very Poor Poor Good

Very Good Excellent
Your review has been successfully submitted.
Tell us what you think about the notes.

Submit Comment

Students' and Teachers' Reviews


Here's what our users had to say ...

Esoma-KE Member
Indeed I getting Samethng here for sure
Guest User
Woow very interesting
Guest User
very good and understandabld
Guest User
I have really get the way for calculating quadratic formula and equation
Guest User
very good example of someone can understand easily
Esoma-KE Member
Ohh the notes are nice
Guest User
May I get another on of Linear
Guest User
Thanks for good notes