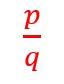Hello Esoma-KE community! If you're able to read this message, you're currently on the previous version of Esoma-KE. Our team is presently in the process of rebranding this platform, and as such, you may observe some variations. At Esoma-KE, our primary objective is to offer you superior quality education.

Change Class FORM THREE

Select Subject | Mathematics

Mathematics English Kiswahili Chemistry Physics Biology Agriculture Business Studies Geography History Religious Studies

Hello guest, kindly login to access unlimited study notes and revision questions.

Create an account / login to help track your progress and unlock more features including additional notes, rapid quizzes, revision questions, virtual library, and the new Esoma Classroom

Surds

A surd can be described as a root whose exact value cannot be found. It is an example of an irrational number; a number which cannot be expressed in the form:

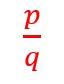
Maths Rule P / Q

In getting the value of a surd, the decimal number obtained is neither recurring nor terminating.
Consider:
√2, √3, √5, √6

Simplification of Surds

Example 1

Simplify: √80

= √(16 x 5)
= √16 x √5
= 4√5

Example 2

Simplify: 3√2 + 4√2 - 5√2

= (3 + 4 - 5)√2
= 2√2

Example 3

Simplify: 5√8 - 2√2

= 5 x √4 x √2 - 2√
= 5 x 2 x √2 - 2√2
= 10√2 - 2√2
= (10 - 2)√2
= 8√2

Rationalizing the Denominator

- Involves writing the denominator as a rational numbers.
Example 4
Rationalize the denominator

Surds - Form 3 Mathematics Example

Surds - Form 3 Mathematics Answer

Hello Guest, Please help review these notes. Why review

Very Poor Poor Good

Very Good Excellent

SORRY, You Need to Be a MEMBER to Review Notes. LOGIN To Continue

Your review has been successfully submitted.

Tell us what you think about the notes.