Esoma-KE Logo
esoma@esomake.co.ke
 

Perimeter, Area, and Volume of Common Shapes and Solids | Primary Mathematics

Perimeter, Area, and Volume of Common Shapes and Solids

  Select Class Primary

Guest Account

Hello Guest, Create an Account or Login to save your progress and get unlimited access to more notes, revision exercises and answers.
Attempt Class 8 & KCPE 2021 Mathematics Questions

Attempt Class 7 Mathematics Questions

Attempt Class 6 Mathematics Questions
Guest Account

Common Geometrical Shapes, Properties, Perimeter, and Area

Last Updated: 16-21-2021 | Esoma-KE

A Rectangle

A Rectangle

Properties of a Rectangle

  1. Opposite sides are equal
  2. Each interior angle is 90° and they all add up to 360°
  3. Diagonals are equal
  4. Diagonals bisect each other but NOT at right angles

Finding the Perimeter of a Rectangle

P = Length + Length + Width + Width
= L + L + W + W
= 2L + 2W or 2(L+W)

Finding the Area of a Rectangle

Area = Length × Width
A = L × W

Example: Perimeter and Area of a Rectangle

A rectangle has a length of 14 cm and a width of 7 cm. What is the perimeter and area of the rectangle?
a) Perimeter
P = 2(L+W) (See above for the complete formula)
P = 2(14 + 7) cm
P = 2(21) cm
P = 42 cm (Do not forget the units)

b) Area
A = L × W
A = 14 × 7
A = 98cm2

A Square

A Square

Properties of a Square

  1. All sides are equal
  2. Opposite sides are parallel
  3. Each interior angle is a right angle (90°)
  4. The interior angles total up to 360°
  5. Diagonals bisect each other at right angles.
  6. Diagonals measure the same length and bisect interior angles.

Finding the Perimeter of a Square

P = Length + Length + Length + Length
= L + L + L + L
= 4L

Finding the Area of a Square

Area = Length × Length
A = L2

Example: Perimeter and Area of a Square

A square has measures 12 cm on one side. What is the perimeter and area of the square?
a) Perimeter
P = 4L (See above for the complete formula)
P = 4 x 12
P = 48 cm (Do not forget the units)

b) Area
A = L × L or L2
A = 12 × 12
A = 144cm2

A Parallelogram

A Parallelogram

Properties of a Parallelogram

  1. Opposite sides are equal and parallel
  2. Opposite angles are equal
  3. Diagonals bisect each other
  4. Diagonals are not equal
  5. Adjacent angles are supplementary (add up to 180°)

Finding the Perimeter of a Parallelogram

P = 2(Base + Height)

Finding the Area of a Parallelogram

Area = Base × Height
A = b x h

A Rhombus

A Rhombus

Properties of a Rhombus

  1. All sides are equal
  2. Opposite sides are parallel
  3. Opposite angles are equal
  4. Diagonals bisect each other at 90°
  5. Diagonals bisect the interior angles

Finding the Perimeter of a Rhombus

P = 2(Base + Height)

Finding the Area of a Rhombus

Area = Base × Height
A = b x h

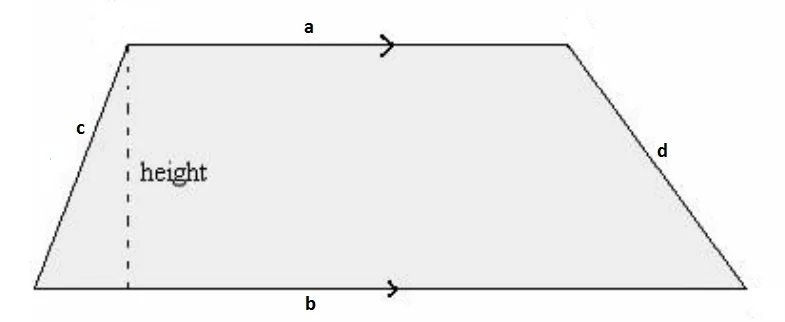
A Trapezium

A Trapezium

Properties of a Trapezium

  1. The sum of the interior angles is 360°
  2. Has a pair of parallel lines which are not of the same length
  3. Has a perpendicular height joining the two parallel lines

Finding the Perimeter of a Trapezium

P = a + b + c + d

Finding the Area of a Trapezium

A = ½ × (sum of parallel lines) × height
A = ½ × (a + b) × h
A = ½h (a + b)

Example: Area of a Trapezium

The parallel sides of a trapezium measure 10cm by 18cm respectively. If the distance between the parallel sides is 8cm, what is the area of the trapezium in cm2?
a) Area
A = ½h (a + b)
A = ½ x 8 x (10 + 18)
A = ½ x 8 x 28
A = 112cm2

A Triangle

a) Right-angled triangle (Pythagorean relationship)

A Right-angled Triangle
  1. a2 + b2 = c2
  2. a2 = c2 - b2
  3. b2 = c2 - a2

b) Equilateral Triangle

An Equilateral Triangle
  1. All sides are equal
  2. All angles are equal
  3. The sum of interior angles is 180°
  4. Each angle measures 60°

c) Isosceles Triangle

An Isosceles Triangle
  1. Only two sides are equal
  2. Base angles are equal

Area and Perimeter of a triangle

An Triangle

Finding the Perimeter of a triangle

P = Sum of the Sides a, b, and c
P = a + b + c

Finding the Area of a triangle

Area = ½ base x height
Area = ½ b x h

A Circle

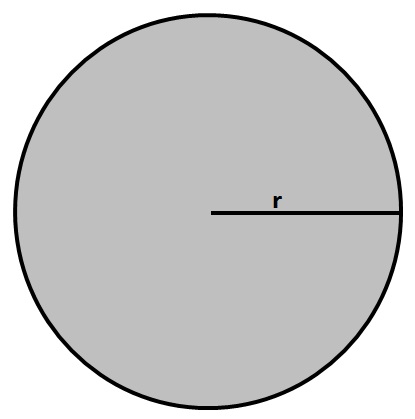
a) A Full Circle

A Full Circle

Finding the Area of a circle

Area = π x radius x radius
A = π x r x r
A = πr2
(π = 22/7 or 3.1429 [4 d.p])

Finding the Perimeter of a circle (Circumference)

Perimeter = π x diameter
Diameter = r + r
P = π x 2r
P = πd or 2πr
(π = 22/7 or 3.1429 [4 d.p])

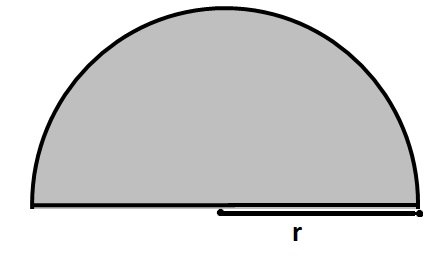
b) A Half Circle

A Half Circle

Finding the Area of a half circle

Area = (π x radius x radius) ÷ 2
A = (π x r x r) ÷ 2
A = 1/2 πr2

Finding the Perimeter of a half circle

Perimeter = Circumference + Diameter
Perimeter = (π x diameter) ÷ 2 + Diameter
Diameter = r + r
P = 1/2πd + d

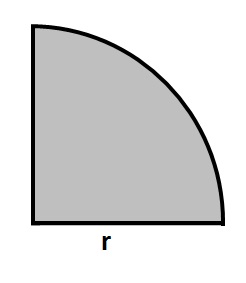
c) A Quarter Circle

A Quarter Circle

Finding the Area of a Quarter circle

Area = (π x radius x radius) ÷ 4
A = (π x r x r) ÷ 4
A = 1/4 πr2

Surface Area of Common Solids

Surface Area of a Cylinder

A Cylinder

If closed on both ends:

Total Surface Area = Area of Circular ends + Area of the Curved Surface
TSA = 2πr2 + πdh

If open on one end:

TSA = πr2 + πdh

If open on both ends:

TSA = πdh

Volume of a Cylinder

Volume = Base Area x Height
V = πr2 x height
V = πr2h

Surface Area of a Cube

A Cube
Total Surface Area = Total Area of all Six Faces
= 6 x L x L
= 6L2 - if closed
= 5L2 - if open on one end

Volume of a Cube

Volume = Base Area x Height
V = length x width x height
V = L x w x h

Surface Area of a Cuboid

A Cuboid
Total Surface Area = Total Area of all Six Faces
= 2 (L x W) + 2 (L x H) + 2 (W x H) - if closed
= L x W + 2 (L x H) + 2 (W x H) - if open on one end

Surface Area of a Triangular prism

A Triangular prism
Total Surface Area = Total Area of all five Faces of the Prism
= TSA of 2 Triangles and TSA of 3 Rectangles

Perimeter and Surface Area of Complex Shapes

Complex shapes are made up of two or more common shapes.
To find the perimeter and surface area, you will have to apply different formulas and sum them to get the total.
For Instance, look at the objects below:

Example 1

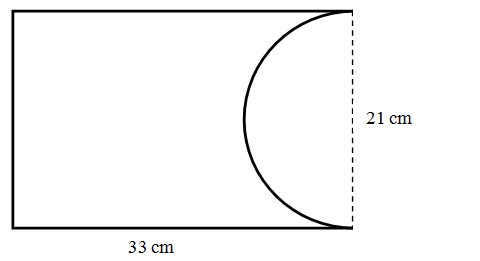
A Complex Object

Calculating the Perimeter

How many common shapes make up this object?
There are 2: A Rectangle and a Semi-circle.
Perimeter of the semi circle
P = 1/2πd
P = 1/2 x 22/7 x 21
P = 33 cm
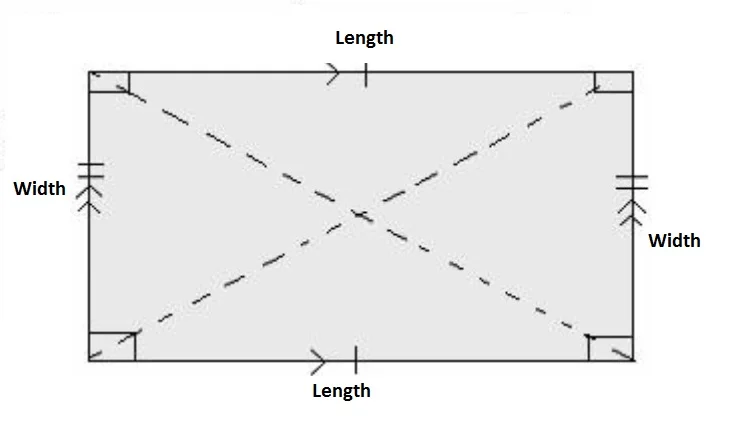
Perimeter of the 3 sides of the rectangle
P = L + W + L
P = 33 + 21 + 33
P = 87cm
Total Perimeter:
T.P = 33 + 87
120 cm

Example 2

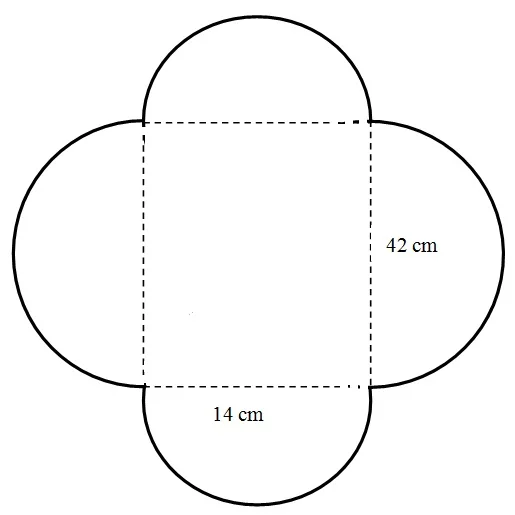
A Complex Object

Calculating the Perimeter

How many common shapes make up this object?
There are 4 Semi-circles.
Perimeter of the small semi circles
P = 1/2πd
P = 1/2 x 22/7 x 14
P = 22 cm (For 1 semi circle)
22cm + 22cm
= 44 cm
Perimeter of the larger semi circles
P = 1/2 x 22/7 x 42
P = 66 cm (For 1 semi circle)
66 + 66
= 132 cm
Total Perimeter:
T.P = 44 + 132
176 cm

Applications of Perimeter

Example 3

The diameter of a wheel is 0.56m. How many kilometres does it cover when it makes 2,000 revolutions?

Solution

1 revolution = πd (the circumference)
2000 revolutions = 2000 πd;
= (2000 x 22/7 x 0.56) m
= 3 520m
We convert m to km (1000m = 1km)
= 3520 ÷ 1000
= 3.52 km